这段时间偶然刷到一道我还是高中生的时候就见过的看起来简单但是实际上并不算很简单的数学题,想着现在的知识储备应该足够解决这道题了,所以记录一下.
原问题
已知\(x,y,z\)为三正整数且满足
$$
\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=4
$$
求\(x,y,z\).
解答
方程两边乘上\((x+y)(x+z)(y+z)\)可以得到:
$$
x(x+y)(x+z)+y(x+y)(y+z)+z(x+z)(y+z)=4(x+y)(x+z)(y+z)
$$
展开后整理可得:
$$
x^{3} – 3 x^{2} y – 3 x y^{2} + y^{3} – 3 x^{2} z – 5 x y z – 3 y^{2} z – 3 x z^{2} – 3 y z^{2} + z^{3}=0
$$
使用sagemath的EllipticCurve_from_cubic方法可以得到:
Scheme morphism:
From: Projective Plane Curve over Rational Field defined by x^3 - 3*x^2*y - 3*x*y^2 + y^3 - 3*x^2*z - 5*x*y*z - 3*y^2*z - 3*x*z^2 - 3*y*z^2 + z^3
To: Elliptic Curve defined by y^2 + x*y = x^3 + 69*x^2 + 1365*x + 8281 over Rational Field
Defn: Defined on coordinates by sending (x : y : z) to
(-x - z : x : 6/91*x - 1/91*y + 6/91*z)也就是令\(X=-x-z,Y=x,Z=\frac{6}{91}x-\frac{1}{91}y+\frac{6}{91}z\)可以得到曲线:
$$
Y^2+XY=X^3+69X^2+1365X+8281
$$
那么我们只需要搜索该曲线上的有理点\((X_r/Z_r,Y_r/Z_r,1)\),并计算:
$$
\begin{cases}
x=Y_r\\
y=-91(Z_r+\frac{6}{91}X_r)=-91Z_r-6X_r\\
z=-X_r-Y_r
\end{cases}
$$
判断\(x,y,z\)是否均大于\(0\)即可:
R.<x, y, z> = QQ[]
eq = x*(x+y)*(x+z)+y*(x+y)*(y+z)+z*(x+z)*(y+z)-4*(x+y)*(x+z)*(y+z)
# print(EllipticCurve_from_cubic(eq, morphism=True))
E = EllipticCurve_from_cubic(eq, morphism=False)
print(E)
G = E.gens()[0]
tmp = G
while True:
tmp = tmp + G
Z = lcm(tmp.x().denominator(), tmp.y().denominator())
X = tmp.x().numerator() * (Z / tmp.x().denominator())
Y = tmp.y().numerator() * (Z / tmp.y().denominator())
solx = Y
soly = -91*Z - 6*X
solz = -X-Y
if solx > 0 and soly > 0 and solz > 0 and eq(solx, soly, solz) == 0:
print(f'x = {solx}\ny = {soly}\nz = {solz}')
break搜索可以得到其中一组解:
$$
\begin{aligned}
x &= 154476802108746166441951315019919837485664325669565431700026634898253202035277999\\
y &= 4373612677928697257861252602371390152816537558161613618621437993378423467772036\\
z &= 36875131794129999827197811565225474825492979968971970996283137471637224634055579\\
\end{aligned}
$$
推广
我们尝试将问题推广到
$$
\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=n
$$
其中\(n\)是正整数,那么我们可以通过EllipticCurve_from_cubic方法得到可以将上述方程转换为一条齐次有理椭圆曲线的坐标变换,对不同的\(n\),找规律可以总结出坐标变换的形式应该均为:
$$
\begin{cases}
X=-x-z\\
Y=x\\
Z=\frac{n+2}{m}x-\frac{1}{m}y+\frac{n+2}{m}z
\end{cases}
$$
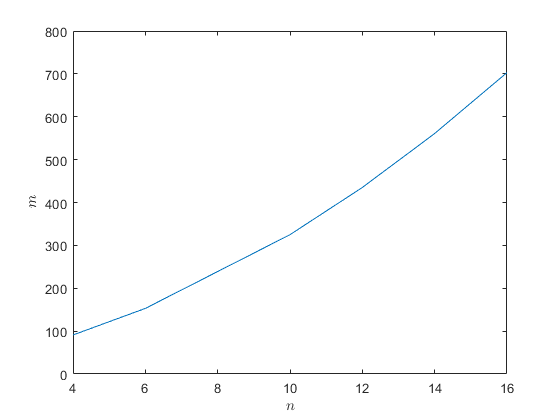
其中\(m\)与\(n\)的关系暂不确定,尝试列出\(n=4, 6,10,12,14,16\)时\(m\)与\(n\)的关系如下:
| \(n\) | 4 | 6 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|
| \(m\) | 91 | 153 | 325 | 435 | 561 | 703 |
使用matlab作图如下:
似乎存在一定关系,尝试采用拉格朗日插值法进行多项式插值可以得到\(m_L(n) = 2n^{2}+11n+15\),生成多组数据测试发现测试点均在插值曲线上,所以可以初步确定\(m=2n^2+11n+15\),从而可以初步确定坐标变换为:
$$
\begin{cases}
X=-x-z\\
Y=x\\
Z=\frac{n+2}{2n^2+11n+15}x-\frac{1}{2n^2+11n+15}y+\frac{n+2}{2n^2+11n+15}z
\end{cases}
$$
利用高斯消元法可以得到:
$$
\begin{cases}
x = Y\\
y = -(n+2)X-(2n^2+11n+15)Z\\
z = -X-Y
\end{cases}
$$
将上述变换代回方程中整理可得:
$$
(4n^4+44n^3+181n^2+330n+225)Z^3+(4n^3+36n^2+107n+105)XZ^2+(n^2+9n+17)X^2Z+X^3-XYZ-Y^2Z=0
$$
两边均除以\(Z^3\)并令\(x’=X/Z,y’=Y/Z\)可以得到一非齐次坐标下的椭圆曲线方程:
$$
y’^2+x’y’=x’^3+(n^2+9n+17)x’^2+(4n^3+36n^2+107n+105)x’+(4n^4+44n^3+181n^2+330n+225)
$$
所以很显然,坐标变换
$$
\begin{cases}
X=-x-z\\
Y=x\\
Z=\frac{n+2}{2n^2+11n+15}x-\frac{1}{2n^2+11n+15}y+\frac{n+2}{2n^2+11n+15}z
\end{cases}
$$
可以将方程:
$$
\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=n
$$
转换为椭圆曲线:
$$
y’^2+x’y’=x’^3+(n^2+9n+17)x’^2+(4n^3+36n^2+107n+105)x’+(4n^4+44n^3+181n^2+330n+225)
$$
那么我们可以利用上述关系来求解任意\(n\in\mathbb{N}_+\)时的:
$$
\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=n
$$
根据上述分析,可以得到更通用的求解脚本如下:
n = 28
R.<x, y, z> = QQ[]
check = x/(y+z) + y/(x+z) + z/(x+y) - n
a1 = 1
a2 = n^2 + 9*n + 17
a3 = 0
a4 = 4*n^3 + 36*n^2 + 107*n + 105
a6 = 4*n^4 + 44*n^3 + 181*n^2 + 330*n + 225
E = EllipticCurve(QQ, [a1, a2, a3, a4, a6])
# print(E)
if E.ngens():
# print(E.gens())
G = E.gens()[0]
tmp = G
cnt = 0
while True:
tmp = tmp + G
Z = lcm(tmp.x().denominator(), tmp.y().denominator())
X = tmp.x().numerator() * (Z / tmp.x().denominator())
Y = tmp.y().numerator() * (Z / tmp.y().denominator())
solx = Y
soly = -(n+2)*X - (2*n^2 + 11*n + 15)*Z
solz = -X - Y
g = gcd(gcd(solx, soly), solz)
solx = ZZ(solx / g)
soly = ZZ(soly / g)
solz = ZZ(solz / g)
if solx > 0 and soly > 0 and solz > 0 and check(solx, soly, solz) == 0:
print(f'x = {solx}\ny = {soly}\nz = {solz}')
break
else:
print("No solution found")经过测试,仅在\(n\)为偶数的时候该方程可能有解,具体原因在An interesting equation: x/(y+z)+y/(z+x)+z/(x+y)=4 x,y,z∈Z+中有提及.